[Algorithm/Java] DFS, BFS

1. 깊이 우선 탐색 (DFS)

DFS : Depth-First Search

그래프 이론 중에서 DFS와 BFS라는 것에 대해 배워볼 것입니다

이전의 트리 구조에 이어 이번에도 우선 순위가 적혀있는 노드(Node)가 등장합니다
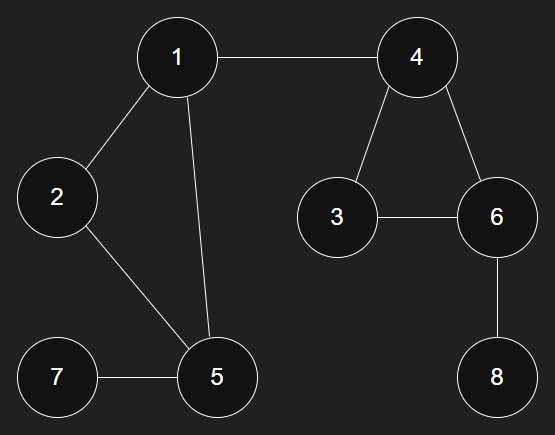
만약 위 이미지처럼 노드가 그려진 그래프가 있을 때, 1번 노드부터 탐색한다고 하면 순서는 어떻게 나오게 될까요

단순하게 직접 그려서 이어보면 [ 1 -> 2 -> 5 -> 7 -> 4 -> 3 -> 6 -> 8 ]이 됩니다
그리고 이 과정을 코드로 구현하면 깊이 우선 탐색 (DFS, Deep-First Search) 알고리즘이 되는거구요

이 알고리즘은 재귀로 푸는 방법과 스택(Stack)으로 푸는 방법으로 2가지가 있습니다

---

1-1. 재귀로 푸는 방법

// 그래프 예시
// 0번 노드는 없기 때문에 {}로 표시
static int[][] graph = { {}, {2, 5, 4}, {1, 5}, {4, 6}, {1, 3, 6}, {1, 7}, {3, 4, 8}, {5}, {6} };

1번부터 차례대로 어떤 숫자의 노드와 연결되어 있는지의 배열을 담은 그래프를 2차원 배열로 표현해봤습니다
이제 이 그래프를 토대로 재귀를 이용해서 풀어봅시다

1. visited 확인
   • 어떤 노드를 지나쳤는지 확인하기 위해 visited 배열을 만들어줍니다
   • 노드 1번부터 8번까지 확인할 것이기 때문에 new boolean[9]로 초기화하면 되겠습니다
2. for문으로 graph의 1번 노드부터 확인
   for (int node: graph[index])를 이용하여 방문한 노드와 인접한 노드에 접근합니다
3. 재귀 사용 1~2번 과정을 dfs(index) 함수로 구현했다면 2번에서 찾은 인접한 노드의 값으로 재귀 함수를 호출합니다

public class Main {

    static boolean[] visited = new boolean[9];
    static int[][] graph = { {}, {2, 4, 5}, {1, 5}, {4, 6}, {1, 3, 6}, {1, 7}, {3, 4, 8}, {5}, {6} };

    public static void dfs(int index) {

        visited[index] = true;
        System.out.print(index + " -> ");

        for (int node : graph[index]) {
            if (!visited[node]) {
                dfs(node);
            }
        }
    }

    public static void main(String[] args) {
        dfs(1);
    }
}

// 출력 결과 : "1 -> 2 -> 5 -> 7 -> 4 -> 3 -> 6 -> 8 -> "

---

1-2. Stack으로 푸는 방법

재귀와 비슷하게 visitied를 활용해서 풀면 됩니다

import java.util.Stack;

public class Main {

    static boolean[] visited = new boolean[9];
    static int[][] graph = { {}, {2, 4, 5}, {1, 5}, {4, 6}, {1, 3, 6}, {1, 7}, {3, 4, 8}, {5}, {6} };

    static Stack<Integer> stack = new Stack<>();

    public static void main(String[] args) {

        // 첫 노드를 push 하고 방문 여부 true
        stack.push(1);

        while(!stack.isEmpty()) {
            int nodeIndex = stack.pop();

            // pop 시점에 방문 체크
            if (!visited[nodeIndex]) {
                visited[nodeIndex] = true;
                System.out.print(nodeIndex + " -> ");

                for (int index: graph[nodeIndex]) {
                    if (!visited[index]) {
                        stack.push(index);
                    }
                }
            }
        }
    }
}

//출력 결과 : "1 -> 5 -> 7 -> 4 -> 6 -> 8 -> 3 -> 2 -> "

단, 위처럼 사용하면 LIFO 특성을 가진 스택에서 큰 숫자부터 pop을 하기 때문에 결과가 다르게 나옵니다

만약 재귀 예시처럼 작은 숫자부터 for문이 돌아가도록 설정하면 됩니다
또는 배열의 값이 내림차순으로 들어가도록 해도 되구요

import java.util.Stack;

public class Main {

    static boolean[] visited = new boolean[9];
    static int[][] graph = { {}, {2, 4, 5}, {1, 5}, {4, 6}, {1, 3, 6}, {1, 7}, {3, 4, 8}, {5}, {6} };

    static Stack<Integer> stack = new Stack<>();

    public static void main(String[] args) {

        // 첫 노드를 push 하고 방문 여부 true
        stack.push(1);

        while(!stack.isEmpty()) {
            int nodeIndex = stack.pop();

            if (!visited[nodeIndex]) {   // pop 시점에 방문 체크
                visited[nodeIndex] = true;
                System.out.print(nodeIndex + " -> ");

                // 재귀 DFS 순서와 맞추려면 역순으로 push
                for (int i = graph[nodeIndex].length - 1; i >= 0; i--) {
                    int next = graph[nodeIndex][i];
                    if (!visited[next]) {
                        stack.push(next);
                    }
                }
            }
        }
    }
}

2. 너비 우선 탐색 (BFS)

BFS : Breadth-First Search

DFS는 하나의 노드를 길게 연결하며 탐색했었죠, BFS는 살짝 다르지만 내용은 거의 비슷합니다
시작 노드에서 가장 가까운 노드를 먼저 모두 방문하며 탐색하는 알고리즘이라 보면 될 것 같습니다

Stack을 이용한 DFS를 이해했다면… 거의 Queue로만 바꿔주면 BFS가 됩니다, 매우 간단하지 않나요

import java.util.LinkedList;
import java.util.Queue;

public class Main {

    static boolean[] visited = new boolean[9];
    static int[][] graph = { {}, {2, 4, 5}, {1, 5}, {4, 6}, {1, 3, 6}, {1, 7}, {3, 4, 8}, {5}, {6} };

    static Queue<Integer> queue = new LinkedList<>();

    public static void main(String[] args) {

        // 첫 노드를 add 하고 방문 여부 true
        queue.add(1);

        while(!queue.isEmpty()) {
            int nodeIndex = queue.poll();

            if (!visited[nodeIndex]) {
                visited[nodeIndex] = true;
                System.out.print(nodeIndex + " -> ");

                for (int index: graph[nodeIndex]) {
                    if (!visited[index]) {
                        queue.add(index);
                    }
                }
            }
        }
    }
}

//출력 결과 : "1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7 -> 8 -> "