[Algorithm/Java] 트리 (Tree)

1. 트리 (Tree)

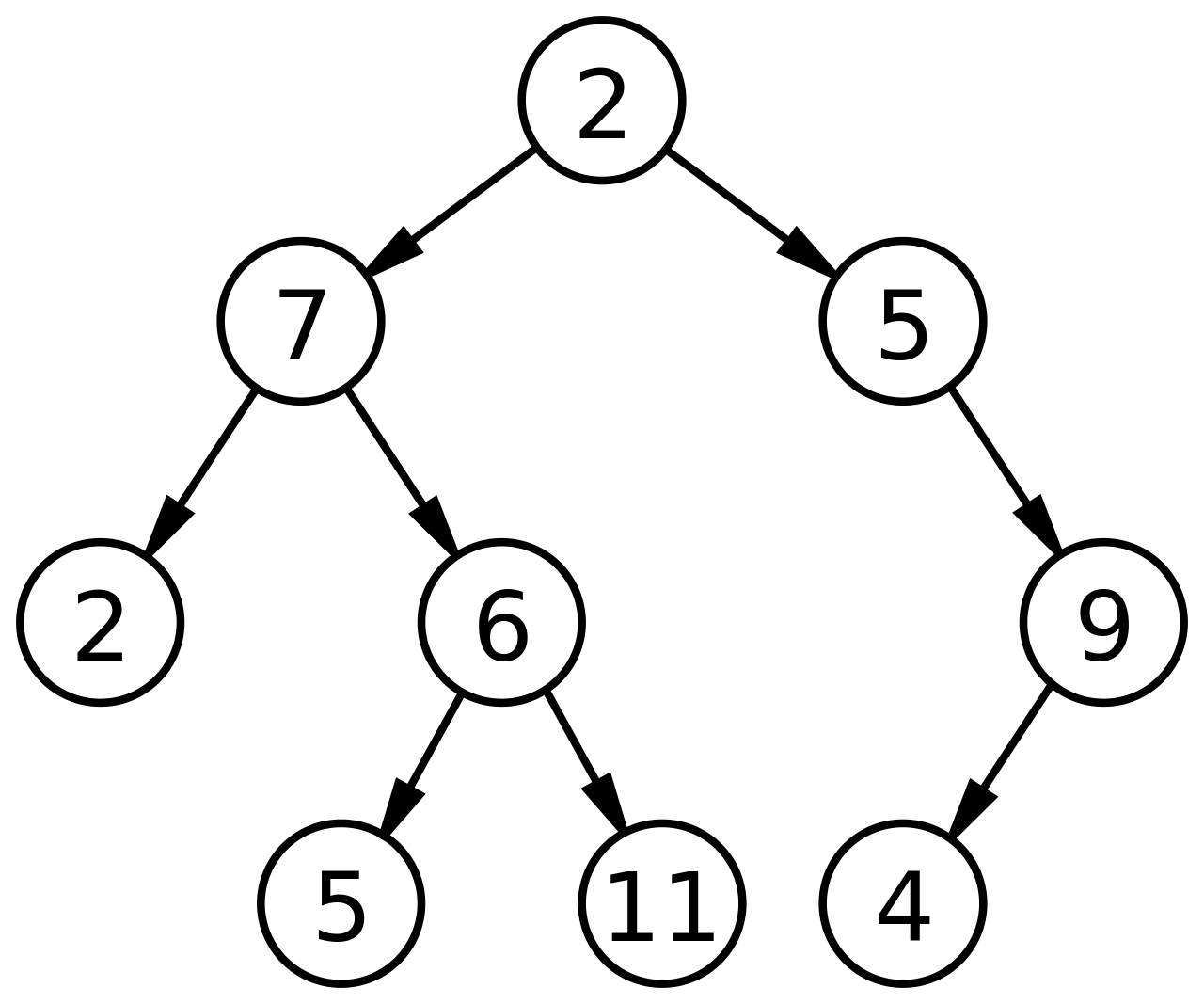
트리 구조는 노드(Node)로 이루어진 자료 구조입니다
이름처럼 구조를 그려보고 거꾸로 바라보면 나무처럼 생긴 것이 특징이기도 하죠

트리는 비선형이기 때문에, 순서를 가지는 자료구조인 List같은 것과 다르게 계층적인 자료구조라고 보면 되겠습니다
그리고 노드는 0개 이상의 하위 노드(=자식 노드)를 가리키고 있다는 특징이 있습니다

---

2. 트리 순회 (백준 1991)

백준 1991 - 트리 순회

• 문제
  
  • 이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오
  • 예시 :
    • 전위 순회 : ABDCEFG
    • 중위 순회 : DBAECFG
    • 후위 순회 : DBEGFCA

위 그림처럼 노드마다 최대 2개의 자식 노드를 가지면 이진 트리(Binary Tree)라고도 합니다

각 노드를 지나갈 때마다 [ 1. LEFT 자식 노드로 이동 / 2. ROOT 노드 출력 / 3. RIGHT 자식 노드로 이동 ]
3가지 선택지를 수행할 수 있는데 이 3가지의 실행 순서에 따라 전위, 중위, 후위 순회로 표현할 수 있습니다

• 전위 순회 : ROOT -> LEFT -> RIGHT
• 중위 순회 : LEFT -> ROOT -> RIGHT
• 후외 순회 : LEFT -> RIGHT -> ROOT

위 문제의 예시를 따라 문제의 이미지에서 그려보면 어느정도 감이 올 것 같습니다

---

3. 문제 풀이

static class Node {
    char value;
    Node left;
    Node right;

    public Node(char value) {
        this.value = value;
    }
}

우선 노드(Node) 클래스를 하나 만들어봅시다
각 노드에는 LEFT 또는 RIGHT 노드의 정보도 담겨져있고 그 노드에 있는 문자도 포함되어있겠죠

이제 각 노드마다 자식 노드를 참조하도록 설정해봅시다

public static void insertNode(Node root, char value) {
    if (root.value == value) {
        if (left != '.') root.left = new Node(left);
        if (right != '.') root.right = new Node(right);
    }
    else {
        if (root.left != null) insertNode(root.left, value, left, right);
        if (root.right != null) insertNode(root.right, value, left, right);
    }
}

• 만약 root 노드인 경우
  • ”.”으로 표시되지 않았다면 (노드가 있다고 하면) 새로운 노드를 만들어서 붙여줍니다
• 만약 root 노드가 아니면 자식 노드로 넘어가면서 탐색합니다

이러한 방법으로 노드를 삽입하는 경우 기본적으로 가장 상위의 노드 1개는 만들고 시작해야 합니다
여기서는 문제처럼 ‘A’노드가 첫 시작이라고 명시되어 있습니다

public static void preorder(Node node) {
    if (node == null) return;
    sb.append(node.value);
    preorder(node.left);
    preorder(node.right);
}

public static void inorder(Node node) {
    if (node == null) return;
    inorder(node.left);
    sb.append(node.value);
    inorder(node.right);
}

public static void postorder(Node node) {
    if (node == null) return;
    postorder(node.left);
    postorder(node.right);
    sb.append(node.value);
}

트리 구조를 완성하였다면 이제 각각의 순회 메서드를 만들어줍니다
순회하는 방법은 재귀 함수를 사용하면 되겠습니다

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    static class Node {
        char value;
        Node left;
        Node right;

        public Node(char value) {
            this.value = value;
        }
    }

    static StringBuilder sb = new StringBuilder();

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());

        // 가장 상위에 있는 첫 노드 생성
        Node head = new Node('A');

        for (int i = 0; i < N; i++) {
            String[] str = br.readLine().split(" ");
            char value = str[0].charAt(0);
            char left = str[1].charAt(0);
            char right = str[2].charAt(0);

            insertNode(head, value, left, right);
        }

        preorder(head);
        sb.append("\n");

        inorder(head);
        sb.append("\n");

        postorder(head);
        sb.append("\n");

        bw.write(sb+"\n");
        bw.flush();

        br.close();
        bw.close();
    }

    public static void insertNode(Node root, char value, char left, char right) {
        // LEFT 또는 RIGHT 자식 노드 생성 후 연결
        if (root.value == value) {
            if (left != '.') root.left = new Node(left);
            if (right != '.') root.right = new Node(right);
        }
        // 만약 value값이 다른 경우 자식 노드를 탐색한 뒤 노드 삽입
        else {
            if (root.left != null) insertNode(root.left, value, left, right);
            if (root.right != null) insertNode(root.right, value, left, right);
        }
    }

    // 전위 순회
    public static void preorder(Node node) {
        if (node == null) return;
        sb.append(node.value);
        preorder(node.left);
        preorder(node.right);
    }

    // 중위 순회
    public static void inorder(Node node) {
        if (node == null) return;
        inorder(node.left);
        sb.append(node.value);
        inorder(node.right);
    }

    // 후위 순회
    public static void postorder(Node node) {
        if (node == null) return;
        postorder(node.left);
        postorder(node.right);
        sb.append(node.value);
    }
}

이 방법 외에도 노드를 삽입하는 방법이나 노드 클래스를 정하는 방법은 여러가지가 있으니
자료를 찾아보면서 비교해보고 사용하면 좋을 것 같습니다